Local Search - Python Notebook

Local search is an optimization technique used to find a solution to a problem by iteratively exploring neighboring solutions. It starts with an initial solution and makes small changes to it in order to find a better solution. The process continues until no better neighboring solutions can be found.

Hill Climbing Algorithm¶

Some basic libraries we will need.

import matplotlib.pyplot as plt
import numpy as np
import random
import math

Let’s take a random function for local search,

def fun(x):
    return -((x - 2) ** 2) + 4


li = np.arange(-10, 10)

plt.plot(li, fun(li))
plt.grid()
plt.show()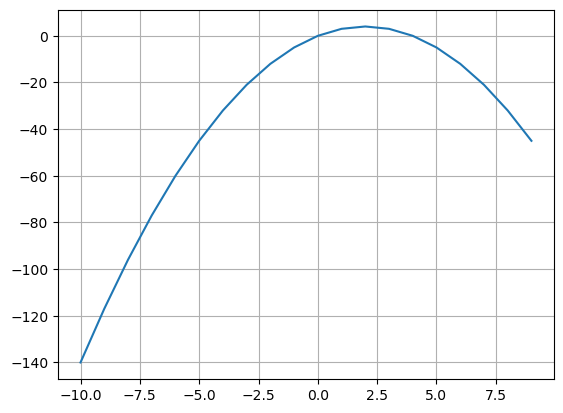

def hill_climb(fun, init, step=1.0, iteration=100):
    x = init
    for i in range(iteration):
        print(f"Step {i+1}: f({x}) -> f({x+step}) OR f({x-step})")
        if fun(x) < fun(x+step):
            x += step
        elif fun(x) < fun(x-step):
            x -= step
        else:
            break
    return x

hill_climb(fun, random.randint(-10, 10), 1.5)

Step 1: f(5) -> f(6.5) OR f(3.5)
Step 2: f(3.5) -> f(5.0) OR f(2.0)
Step 3: f(2.0) -> f(3.5) OR f(0.5)

2.0

Stochastic Hill Climbing¶

This is a variant of the hill climbing algorithm where instead of choosing the best neighbor, we randomly select one of the better neighbors. This helps to avoid getting stuck in local maxima by introducing randomness into the search process. But it’s not guaranteed to find the global maximum.

def stochastic_hill_climb(fun, init, step=1.0, iteration=100):
    x = init
    for i in range(iteration):
        neighbors = [x + step, x - step]
        next_x = random.choice(neighbors)
        # print(f"Step {i+1}: f({x}) -> f({next_x})")
        if fun(next_x) > fun(x):
            x = next_x
    return x

stochastic_hill_climb(fun, random.randint(-10, 10), 1.5)

2.5

First-Choice Hill Climbing¶

def first_choice_hill_climbing(fun, init, step=1.0, max_iterations=1000):
    current_state = init
    for _ in range(max_iterations):
        neighbors = [current_state + step, current_state - step]
        random.shuffle(neighbors)
        for neighbor in neighbors:
            if fun(neighbor) > fun(current_state):
                current_state = neighbor
                break
        else:
            break  # No better neighbor found
    return current_state

first_choice_hill_climbing(fun, random.randint(-10, 10), 1.5)

1.5

Random-Restart Hill Climbing¶

def hill_climb_random(fun, start=-10, stop=10, step=1.0, iteration=100):
    x = random.randint(start, stop)
    di = {}
    for i in range(iteration):
        print(f"Step {i+1}: f({x}) - f({x+step}) - f({x-step})")
        if fun(x) < fun(x+step):
            x += step
        elif fun(x) < fun(x-step):
            x -= step
        else:
            di[x] = fun(x)
            x = random.randint(start, stop)
    print(di)
    return [i for i, j in di.items() if j == max(di.values())][0]

hill_climb_random(fun, -10, 10, 1.5, 5)

Step 1: f(5) - f(6.5) - f(3.5)
Step 2: f(3.5) - f(5.0) - f(2.0)
Step 3: f(2.0) - f(3.5) - f(0.5)
Step 4: f(1) - f(2.5) - f(-0.5)
Step 5: f(2.5) - f(4.0) - f(1.0)
{2.0: 4.0, 2.5: 3.75}

2.0

Simulated Annealing¶

def simulated_annealing(fun, start=-10, stop=10, step=1.0, temparature=100, cooling=0.95):
    x = random.uniform(start, stop)
    best = x
    i = 0
    while temparature > 0.1:
        i += 1
        # Small random move (neighbor)
        x_new = x + random.uniform(-step, step)
        if x_new < start: x_new = start
        if x_new > stop: x_new = stop

        delta = fun(x_new) - fun(x)

        # Accept if better or with probability exp(delta/T)
        if delta > 0 or random.random() < math.exp(delta / temparature):
            x = x_new
            if fun(x) > fun(best):
                best = x

        # print(f"[SA] Step {i}: T={temparature:.2f}, x={x:.2f}, f(x)={fun(x):.2f}")
        temparature *= cooling
    return best

simulated_annealing(fun, -10, 10, 1.0, 100, 0.9)

2.0404275910942093

Local Beam Search¶

def local_beam_search(fun, k=2, start=-10, stop=10, step=1.0, iteration=50):
    # Start with k random states
    states = [random.uniform(start, stop) for _ in range(k)]

    for i in range(iteration):
        neighbors = []
        for s in states:
            neighbors.append(s + step)
            neighbors.append(s - step)

        all_states = states + neighbors

        states = sorted(all_states, key=lambda x: fun(x), reverse=True)[:k]

        print(f"[Beam] Step {i+1}: best={states[0]:.2f}, f(best)={fun(states[0]):.2f}")

    return max(states, key=fun)

local_beam_search(fun, 2, -10, 10, 1.5, 5)

[Beam] Step 1: best=-4.49, f(best)=-38.11
[Beam] Step 2: best=-2.99, f(best)=-20.90
[Beam] Step 3: best=-1.49, f(best)=-8.18
[Beam] Step 4: best=0.01, f(best)=0.04
[Beam] Step 5: best=1.51, f(best)=3.76

1.51048385058147