Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

Searching Problems

In artificial intelligence, searching problems involve finding a solution from a large space of possible solutions. We can categorize it into,

  1. Uninformed Search: These algorithms do not have any additional information about the goal state. Examples include,

    • Breadth-First Search (BFS)

    • Depth-First Search (DFS)

    • DFS Limited

    • Iterative DFS

    • Bidirectional Search

    • Uniform Cost Search (UCS)

  2. Informed Search: These algorithms use heuristics to guide the search process. Examples include,

    • Greedy Best-First Search

    • A* Search

First things first, let’s imagine a tree,

Here is a textual representation of the tree:

A
├── B
│ ├── C
│ │ └── F
│ └── D
└── E

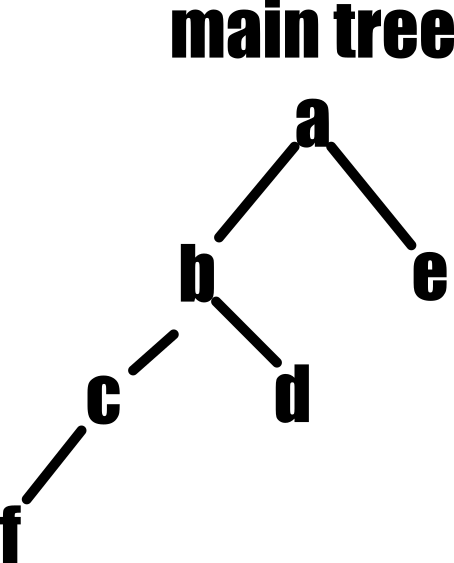
tree = {
        'A': ['B', 'E'],
        'B': ['C', 'D'],
        'C': ['F'],
        'D': [],
        'E': [],
        'F': []
    }

So, if we apply basic search algorithms, we can visualize our output like,

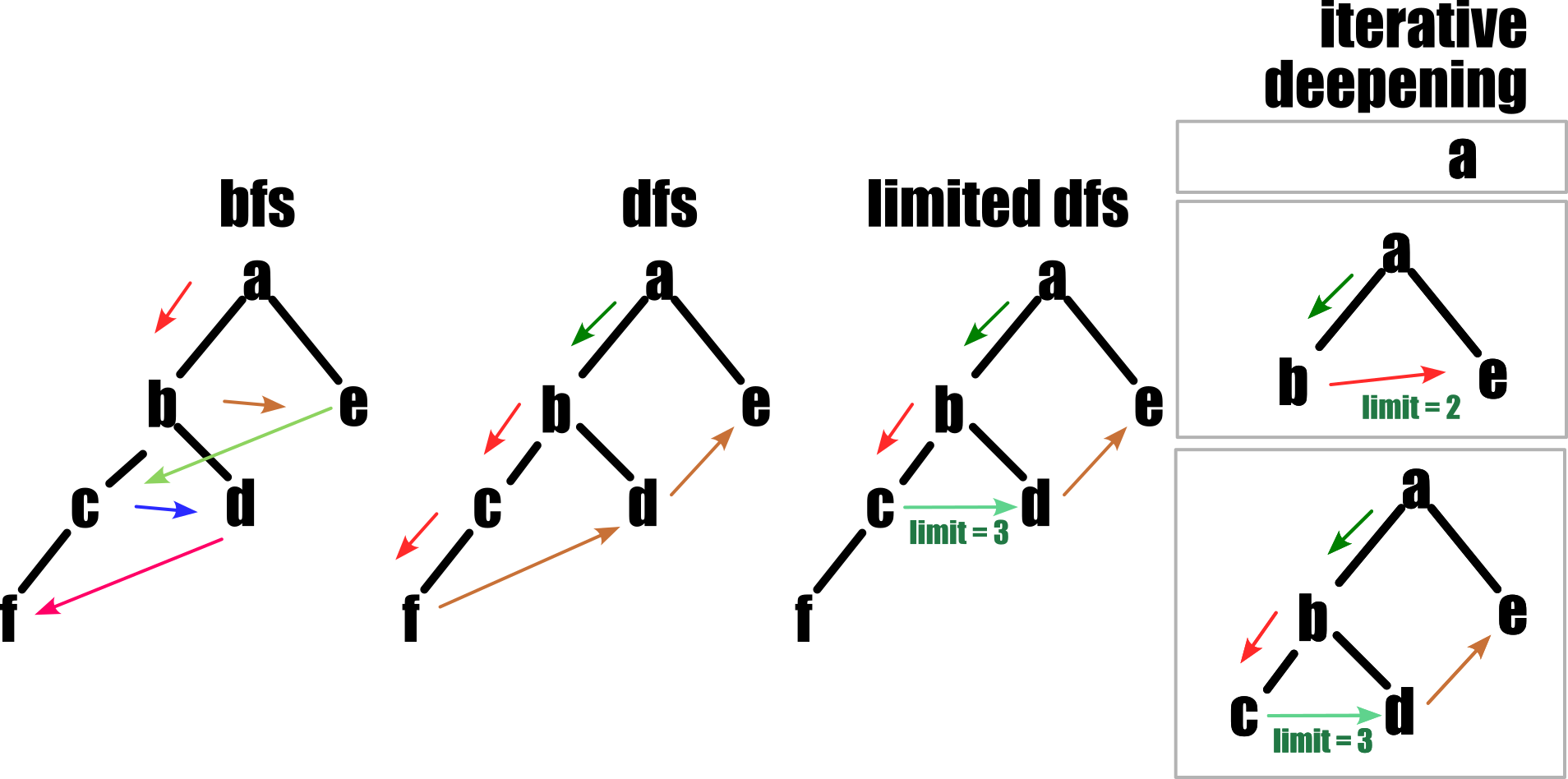
BFS

BFS (Breadth-First Search) is an algorithm for traversing or searching tree or graph data structures. It starts at the root node and explores all neighboring nodes at the present depth prior to moving on to nodes at the next depth level. BFS uses a queue to keep track of nodes to visit next, ensuring that nodes are explored level by level.

from collections import deque

def bfs(tree, start):
    visited = []
    queue = deque([start])

    while queue:
        node = queue.popleft()
        if node not in visited:
            visited.append(node)
            print(node, end=" ")

            for neighbor in tree[node]:
                if neighbor not in visited:
                    queue.append(neighbor)

bfs(tree, 'A')
A B E C D F

DFS

DFS (Depth-First Search) is an algorithm for traversing or searching tree or graph data structures. It starts at the root node and explores as far as possible along each branch before backtracking. DFS uses a stack to keep track of nodes to visit next, ensuring that nodes are explored as deeply as possible before moving on to other branches.

def dfs(tree, start, visited = []):
    if start not in visited:
        print(start, end=" ")
        visited.append(start)
    for node in tree[start]:
        dfs(tree, node, visited)

dfs(tree, 'A')
A B C F D E

DFS Limited

In DFS limited, instead of exploring till the deepest node, we will limit our step number.

def dfs_limited(tree, start, limit, visited=[]):
    if limit <= 0:
        return
    if start not in visited:
        print(start, end=" ")
        visited.append(start)
    for node in tree[start]:
        dfs_limited(tree, node, limit-1, visited)

dfs_limited(tree, 'A', 3)
A B C D E

Iterative DFS

Iterative deepening DFS is a hybrid of DFS and BFS. It repeatedly applies DFS with increasing depth limits until a goal is found. This approach combines the space efficiency of DFS with the completeness of BFS.

def iterative_deepening(tree, start, max_limit):
    for i in range(max_limit):
        print(f"Iteration {i+1} : ", end="")
        dfs_limited(tree, start, i+1, [])
        print()

iterative_deepening(tree, 'A', 4)
Iteration 1 : A 
Iteration 2 : A B E 
Iteration 3 : A B C D E 
Iteration 4 : A B C F D E

Bidirectional search is a graph search algorithm that simultaneously explores the search space from both the initial state and the goal state. The search continues until the two searches meet, thus finding the shortest path more efficiently than traditional unidirectional search methods.

We need a unidirected graph in order to do bidirectional search. Let’s take a look at this graph,

# Unidriected Tree
un_tree = {
        'A': ['B', 'E'],
        'B': ['C', 'D', 'A'],
        'C': ['F', 'B'],
        'D': ['B'],
        'E': ['A'],
        'F': ['C']
    }
from collections import deque
def bidirectional(tree, start, goal):
    if start == goal:
        return None, None

    start_visited = []
    goal_visited = []

    start_queue = deque([start])
    goal_queue = deque([goal])

    while start_queue or goal_queue:
        if start_queue:
            start_node = start_queue.popleft()
            if start_node not in start_visited:
                start_visited.append(start_node)

                for neighbour in tree[start_node]:
                    if neighbour not in start_visited:
                        start_queue.append(neighbour)

        if goal_queue:
            goal_node = goal_queue.popleft()
            if goal_node not in goal_visited:
                goal_visited.append(goal_node)

                for neighbour in tree[goal_node]:
                    if neighbour not in goal_visited:
                        goal_queue.append(neighbour)

        if start_node in goal_visited or goal_node in start_visited:
            return start_visited, goal_visited

print(bidirectional(un_tree, 'A', 'F'))
(['A', 'B', 'E'], ['F', 'C', 'B'])

Here I traverrsed from both sides, but we can do further and build path as well!

UCS

UCS or uniform cost search is a variant of Dijkstra’s algorithm and is used to find the least-cost path from a starting node to a goal node. UCS expands the least costly node in the search space, ensuring that the first time it reaches the goal node, it has found the optimal path.

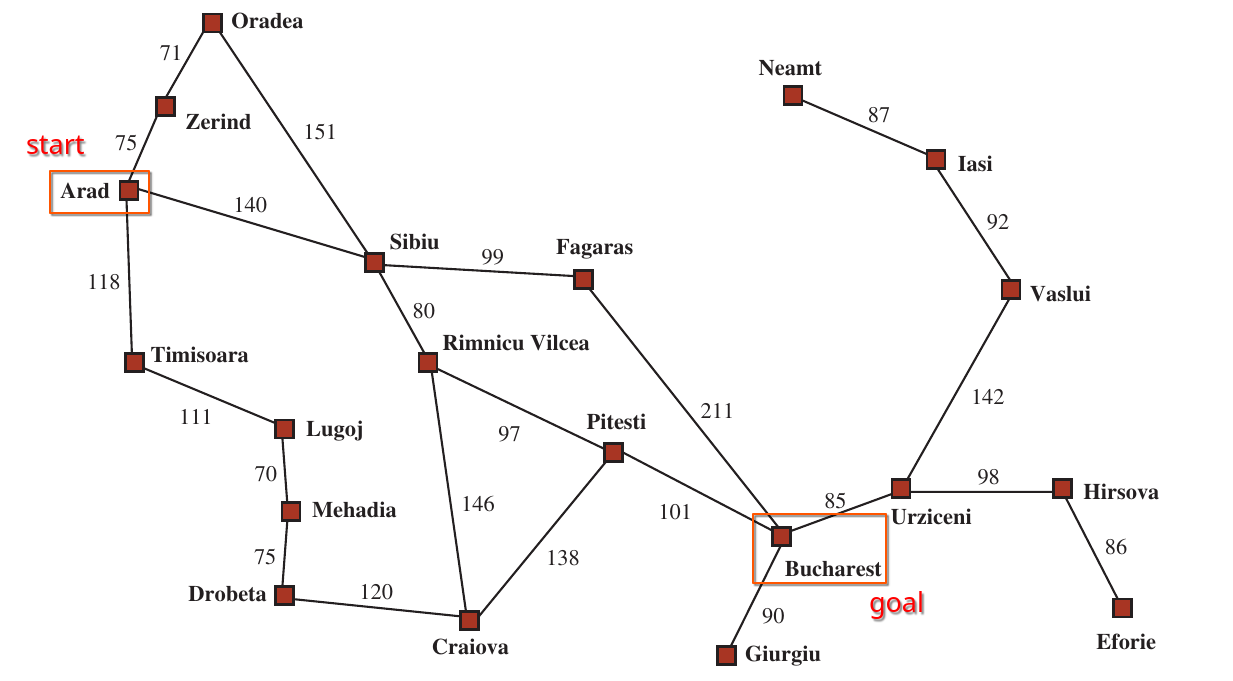
For example, let’s consider a graph (image below in the informed search section),

G = {
    "Arad": [("Zerind", 75), ("Sibiu", 140), ("Timisoara", 118)],
    "Zerind": [("Arad", 75), ("Oradea", 71)],
    "Oradea": [("Zerind", 71), ("Sibiu", 151)],
    "Timisoara": [("Arad", 118), ("Lugoj", 111)],
    "Lugoj": [("Timisoara", 111), ("Mehadia", 70)],
    "Mehadia": [("Lugoj", 70), ("Drobeta", 75)],
    "Drobeta": [("Mehadia", 75), ("Craiova", 120)],
    "Craiova": [("Drobeta", 120), ("Rimnicu Vilcea", 146), ("Pitesti", 138)],
    "Sibiu": [("Arad", 140), ("Oradea", 151), ("Fagaras", 99), ("Rimnicu Vilcea", 80)],
    "Fagaras": [("Sibiu", 99), ("Bucharest", 211)],
    "Rimnicu Vilcea": [("Sibiu", 80), ("Craiova", 146), ("Pitesti", 97)],
    "Pitesti": [("Rimnicu Vilcea", 97), ("Craiova", 138), ("Bucharest", 101)],
    "Bucharest": [("Fagaras", 211), ("Pitesti", 101), ("Giurgiu", 90), ("Urziceni", 85)],
    "Giurgiu": [("Bucharest", 90)],
    "Urziceni": [("Bucharest", 85), ("Hirsova", 98), ("Vaslui", 142)],
    "Hirsova": [("Urziceni", 98), ("Eforie", 86)],
    "Eforie": [("Hirsova", 86)],
    "Vaslui": [("Urziceni", 142), ("Iasi", 92)],
    "Iasi": [("Vaslui", 92), ("Neamt", 87)],
    "Neamt": [("Iasi", 87)],
}

Now let’s try to solve it,

from heapq import heappush, heappop

def ucs(graph, start, goal):
    frontier = []
    heappush(frontier, (0, start, [start])) # path_cost, node, [path]
    best_graph = {start: 0}

    while frontier:
        path_cost, node, path_list = heappop(frontier)
        if node == goal:
            return path_cost, path_list
        for neighbor, neighbor_cost in graph[node]:
            updated_cost = path_cost + neighbor_cost
            if neighbor not in best_graph or updated_cost < best_graph[neighbor]:
                best_graph[neighbor] = updated_cost
                heappush(frontier, (updated_cost, neighbor, path_list + [neighbor]))

    return None, float("inf")

cost, path= ucs(G, "Arad", "Bucharest")
print("Path : ", " -> ".join(path))
print("Cost : ", cost)
Path :  Arad -> Sibiu -> Rimnicu Vilcea -> Pitesti -> Bucharest
Cost :  418

For informed search, let’s consider a map, from Arad to Bucharest. We will use the heuristic function H(n) which is the straight-line distance from any node n to the goal node Bucharest. Here’s a visual representation,

Now let’s define our graph and the heuristic functions,

# Undirected weighted graph: city -> list of (neighbor, distance_km)
G = {
    "Arad": [("Zerind", 75), ("Sibiu", 140), ("Timisoara", 118)],
    "Zerind": [("Arad", 75), ("Oradea", 71)],
    "Oradea": [("Zerind", 71), ("Sibiu", 151)],
    "Timisoara": [("Arad", 118), ("Lugoj", 111)],
    "Lugoj": [("Timisoara", 111), ("Mehadia", 70)],
    "Mehadia": [("Lugoj", 70), ("Drobeta", 75)],
    "Drobeta": [("Mehadia", 75), ("Craiova", 120)],
    "Craiova": [("Drobeta", 120), ("Rimnicu Vilcea", 146), ("Pitesti", 138)],
    "Sibiu": [("Arad", 140), ("Oradea", 151), ("Fagaras", 99), ("Rimnicu Vilcea", 80)],
    "Fagaras": [("Sibiu", 99), ("Bucharest", 211)],
    "Rimnicu Vilcea": [("Sibiu", 80), ("Craiova", 146), ("Pitesti", 97)],
    "Pitesti": [("Rimnicu Vilcea", 97), ("Craiova", 138), ("Bucharest", 101)],
    "Bucharest": [("Fagaras", 211), ("Pitesti", 101), ("Giurgiu", 90), ("Urziceni", 85)],
    "Giurgiu": [("Bucharest", 90)],
    "Urziceni": [("Bucharest", 85), ("Hirsova", 98), ("Vaslui", 142)],
    "Hirsova": [("Urziceni", 98), ("Eforie", 86)],
    "Eforie": [("Hirsova", 86)],
    "Vaslui": [("Urziceni", 142), ("Iasi", 92)],
    "Iasi": [("Vaslui", 92), ("Neamt", 87)],
    "Neamt": [("Iasi", 87)],
}

# Straight-line distances to Bucharest (heuristic)
H = {
    "Arad": 366, "Bucharest": 0, "Craiova": 160, "Drobeta": 242, "Eforie": 161,
    "Fagaras": 176, "Giurgiu": 77, "Hirsova": 151, "Iasi": 226, "Lugoj": 244,
    "Mehadia": 241, "Neamt": 234, "Oradea": 380, "Pitesti": 100,
    "Rimnicu Vilcea": 193, "Sibiu": 253, "Timisoara": 329, "Urziceni": 80,
    "Vaslui": 199, "Zerind": 374,
}

Greedy Best-First Search is an informed search algorithm that uses a heuristic to estimate the cost to reach the goal from a given node. It expands the most promising node based on this heuristic, rather than the actual cost from the start node. This can lead to faster solutions in some cases, but it does not guarantee the optimal solution.

from heapq import heappush, heappop

def greedy_best_first(graph, heuristic, start, goal):
    frontier = []
    heappush(frontier, (heuristic[start], 0, start, [start]))
    best_graph = {start: 0}

    while frontier:
        cost, path_cost, node, path_list = heappop(frontier)
        if node == goal:
            return path_cost, path_list
        for neighbor, neighbor_cost in graph[node]:
            updated_cost = heuristic[neighbor]
            if neighbor not in best_graph or updated_cost < best_graph[neighbor]:
                best_graph[neighbor] = updated_cost
                heappush(frontier, (updated_cost, path_cost + neighbor_cost, neighbor, path_list + [neighbor]))

cost, path= greedy_best_first(G, H, "Arad", "Bucharest") 
print("Path : ", " -> ".join(path))
print("Cost : ", cost)
Path :  Arad -> Sibiu -> Fagaras -> Bucharest
Cost :  450

A* Search is an informed search algorithm that combines the strengths of Uniform Cost Search and Greedy Best-First Search. It uses both the actual cost from the start node to the current node (g(n)) and the estimated cost from the current node to the goal (h(n), the heuristic). The total cost function is f(n) = g(n) + h(n). A* guarantees finding the shortest path if the heuristic is admissible (never overestimates the true cost to the goal). It is widely used in pathfinding and graph traversal due to its optimality and efficiency.

from heapq import heappush, heappop

def a_star(graph, heuristic, start, goal):
    frontier = []
    heappush(frontier, (heuristic[start], 0, start, [start]))
    best_graph = {start: 0}

    while frontier:
        cost, path_cost, node, path_list = heappop(frontier)
        if node == goal:
            return path_cost, path_list
        for neighbor, neighbor_cost in graph[node]:
            updated_cost = path_cost + neighbor_cost + heuristic[neighbor]
            if neighbor not in best_graph or updated_cost < best_graph[neighbor]:
                best_graph[neighbor] = updated_cost
                heappush(frontier, (updated_cost, path_cost + neighbor_cost, neighbor, path_list + [neighbor]))

cost, path= a_star(G, H, "Arad", "Bucharest")
print("Path : ", " -> ".join(path))
print("Cost : ", cost)

Path :  Arad -> Sibiu -> Rimnicu Vilcea -> Pitesti -> Bucharest
Cost :  418
Artifical Intelligence
Artificial Intelligence
Artifical Intelligence
Local Search